円周率とは何だろう？

前回はそんな質問に答えるために記事を書きました。

<前回の記事はこちら>https://note.com/embed/notes/n7a1c2228bbd9

 

皆さんは円周率が何か覚えていますか？

そうですね、”直径”に対する”円周”の割合です。

今回は、円周率に関して出題された東京大学の過去問に迫ります！

実際に出題された問題はこちら↓↓

“円周率が3.05より大きいことを証明せよ。”　(東京大学2003年 理系第6問)

このたった一文です。しかもこれは理系専用の問題。
東京大学なのに意外にシンプルだなと思った方もいるかもしれません。

大学入試問題を解く受験生は分かるかもしれませんが、実は問題文が長い方が解きやすい場合が多いです。今回のように、一行ぐらいのシンプルな問題文だとどう手を付けていいかすら分からない場合が多いので。。

そんな話はさておき、問題に取り掛かりましょう。
まずは手始めに円周率が3より大きいことを証明してみましょう。

実は円周率が3より大きいことは、小学生でも証明できてしまいます。

ヒントは、長さが3のものと円周率を同じ図の中に表せるかどうか、、

分かりましたか？？

円周率は直径に対する円周の比だったので、半径1の半円を考えるとその長さが丁度円周率になります。
その中にこんな三角形を3つ考えるとどうでしょう。

図にするとこんな感じ。

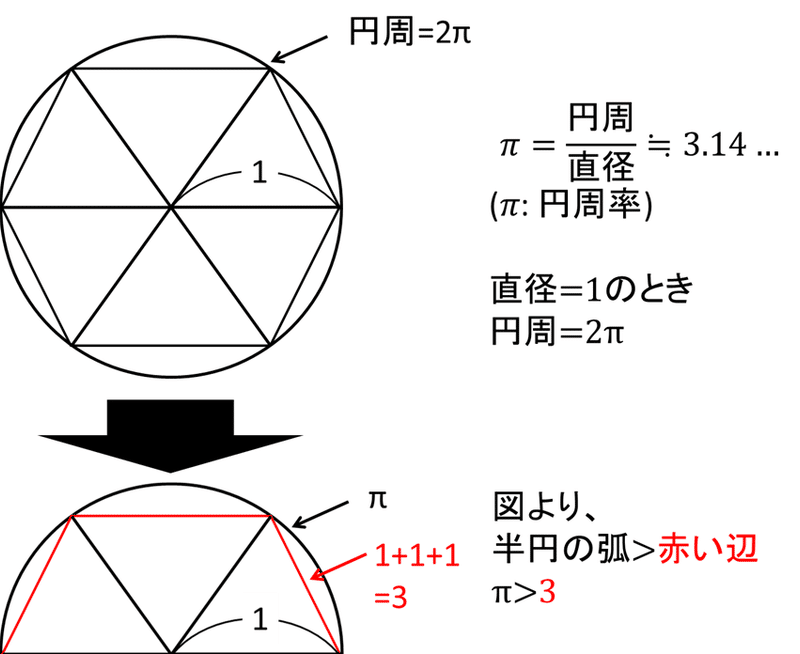
これら三角形はどれも正三角形になるので、それぞれの辺の長さは１です。つまり、半円の中にある3つの三角形の辺を足し合わせると３になります。そして、長さ３の赤い辺より長さπの弧が外側にあるので、π（つまり円周率）は3より大きくなることが証明できます。

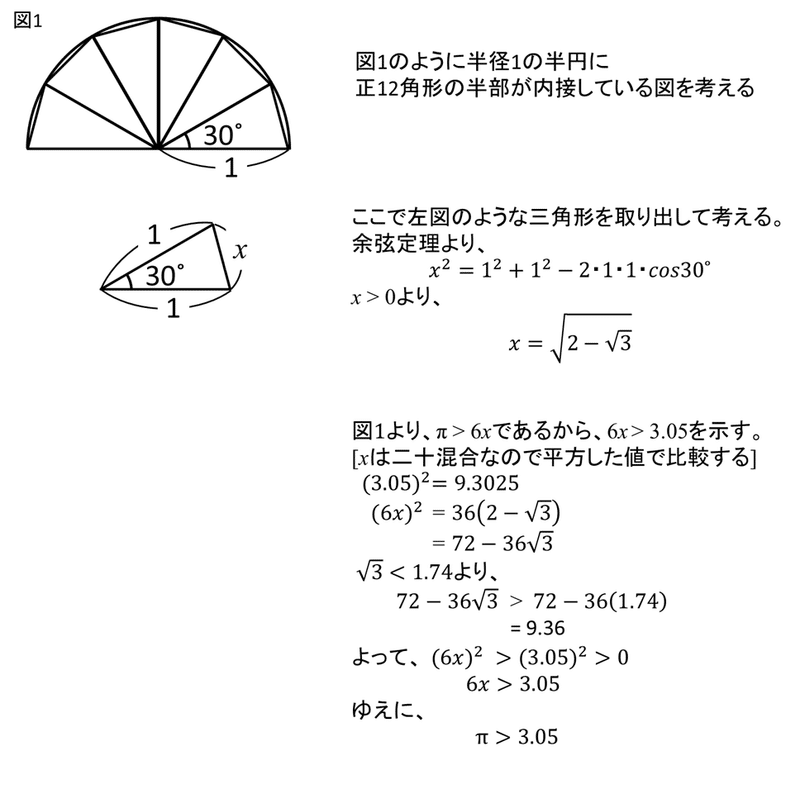
これをさらに6つの三角形に刻んでいき、周の長さを求めると、πが3.05より大きいことを証明することができます。この時、辺の長さを求めるために高校2年で学習する三角関数の知識を使いますが、基本的な考え方は同じです（証明は後述）。

これで皆さんも東大の問題を解くことができるようになりました！（拍手！）

終ってみれば、半円と三角形を書いただけでしたね。しかし、その図形を描き、円周率(3.14..)という値を長さとして表現することこそが最大の関門でした。円周率が何なのかという根本を理解している人でないとこの発想にたどり着くことはできないでしょう。

皆さんは発想できましたか？

日本で最難関と言われている東京大学も難しいばかりが計算ができる人ではなく、教科書に書いてある当たり前のことに疑問を持ち、根本から理解している人を求めているということが読み取れますよね。

問題を解いていくとき、「解答をみれば分かる」はなく、「解答を見なくても答えにたどり着ける」「なぜその発想になるかを説明できる」ようにすることで真の実力はついてきます。

この問題は、そんな勉強の”本質”を問いかけるような問題だと私は感じています。
皆さんも世の中のいろんな”なぜ？”を追究することで物事の”本質”に触れてみてはいかがでしょうか。
日々の生活が一歩豊かになるかもしれませんよ。

（ライター：Fe）

【参考】円周率が3.05以上証明

 

東京大学(理科) (2022年版大学入試シリーズ)